ROBOTICS-MANIPULATOR KINEMATICS 기구학
















Contents
• Introduction
• Link description
• Link connection description
• Convention for affixing frames to link
• Manipulator kinematics
• Actuator space, Joint space and Cartesian space
• Examples : Kinematics of two industrial robots
• Frames with standard names
• WHERE is the tool?
• Computational considerations
Introduction
• 기구학(kinematics)?
움직임을 일으키는 힘, 토크, 관성 등을 고려하지 않고 그 기하학적인 움직임과 시간을 기준으로 한 움직임을 연구하는 학문
• 학습 중점 사항
정지된 위치에서 Manipulator linkage의 위치와 방위를 고려.
특히 Manipulator end-effector의 위치와 방위를 manipulator의 기저부를 기준으로 하는 관절 변수들의 함수로 계산하는 방법을 주로 학습
Link description
• Link?
링크는 Manipulator의 두 이웃 하는 관절 축 사이의 관계를 정의하는 강체(rigid body)
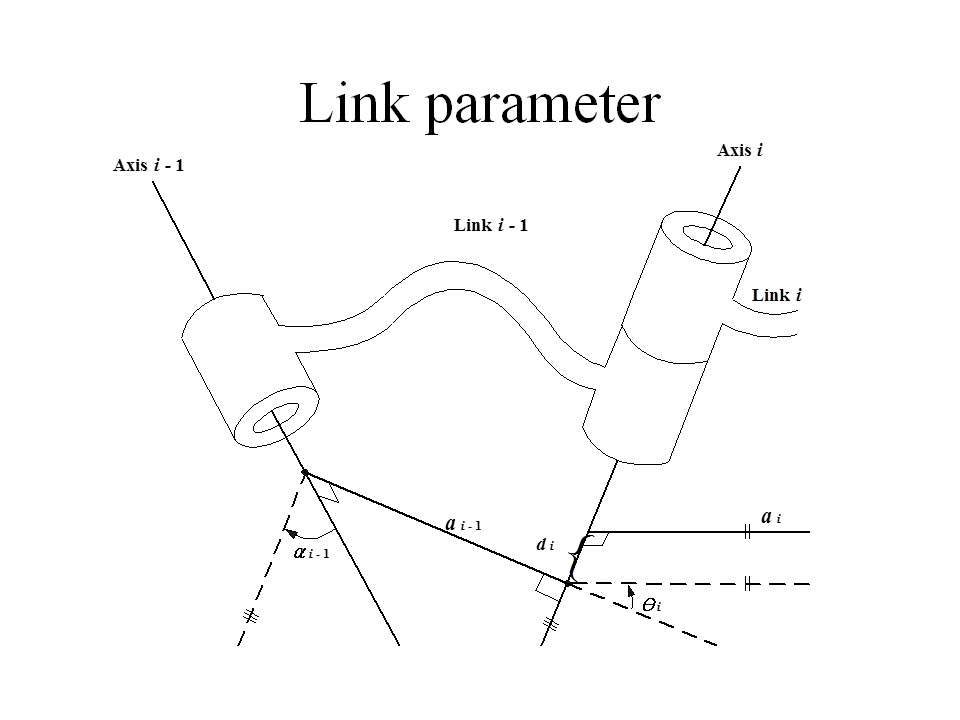
• Link length(링크의 길이 : a i )
The distance of the line which is mutually perpendicular to both axis.
• Link twist (링크의 뒤틀림 : i )
The angle between two line which are projection of both axis onto a
place whose normal is the mutually perpendicular line.
Link connection description
• Link offset (d i)
The signed distance measured along the axis of joint i from the point where a i - 1 intersects the axis to the point where a i intersects the axis.
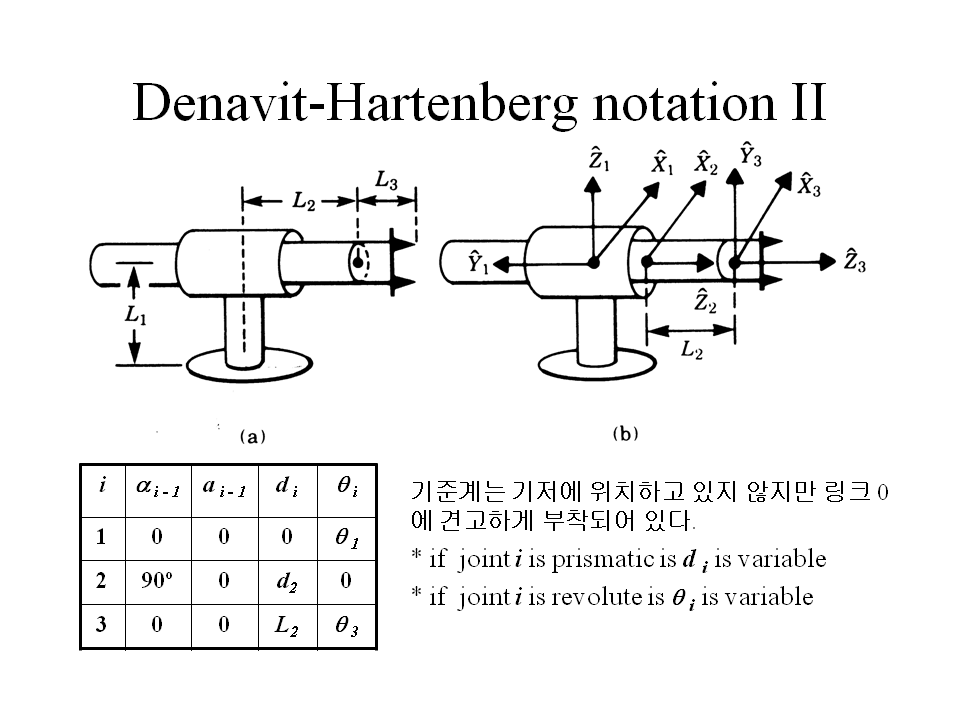
if joint i is prismatic is d i is variable
• Joint angle(i)
The angle made between an extension of a i - 1 and a i measured about the axis of joint i
if joint i is revolute is i is variable
• 4개의 링크인자에 의해 로봇의 기구부를 정의하는 방법
-데나비트-하텐버그 방법
Link parameter
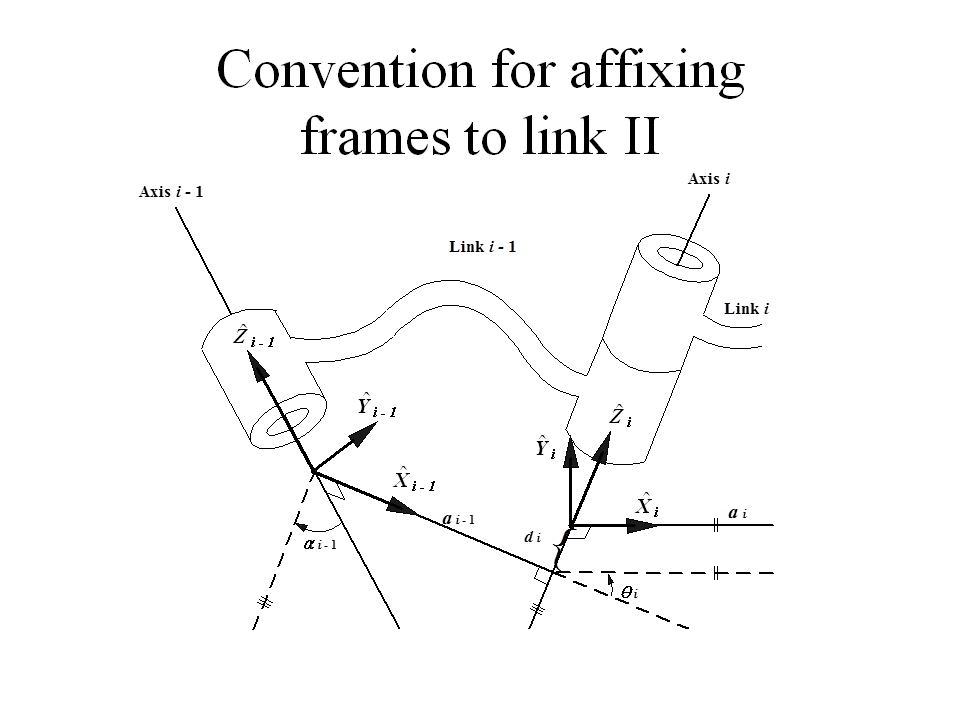
Convention for affixing
frames to link I
• 각 링크들에 대한 위치를 기술하기 위하여 각 링크에 계(Frames)를 정의한다.
• Z i축은 Axis i 에 일치시킨다.
• X i축은 a i (Link length)방향으로 설정한다.
• 원점은 Axis i 와 a i가 수직인 점으로 한다.
• Yi축은 오른손 법칙에 의해 정의한다.
• 링크인자를 링크계의 용어로 정리
- a i = X i 를 따라 측정한 Z i 에서 Z i + 1 까지 거리
- i = X i 를 주위로 측정한 Z i 에서 Z i + 1 사이의 각도
- d i = Z i 를 따라 측정한 X i - 1 에서 X i 까지 거리
- i = Z i 를 주위로 측정한 X i - 1 에서 X i 사이의 각도
Convention for affixing
frames to link II
Denavit-Hartenberg notation I
Denavit-Hartenberg notation II
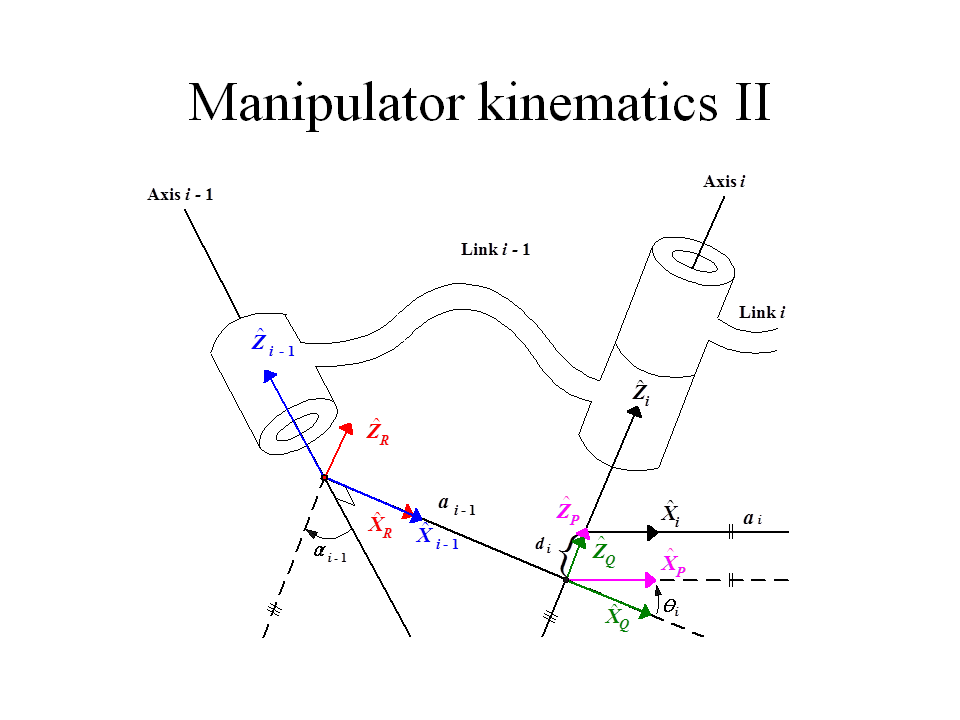
Manipulator kinematics I
• 링크변환의 유도(Derivation of link transformations)
– 계(i)를 계(i -1)에 기준으로 변환을 결정할 때 일반적으로 1개 변수 만의 함수이고 나머지 3개의요소는 기계 설계상 고정
– 기구학적 문제를 n개의 작은 문제 분리해서 해석
– 한 개의 링크요소 만의 함수로 표현
– 일반적으로 링크의 중간 계(Frames)를 {P}, {Q}, {R}로 정의
– 계{i-1}, 계{P}, 계{Q}, 계{R}, 계{i}의 순차적인 연관성으로 링크 i-1 에서 다음링크 i를 표현
i - 1P = i - 1T RT QT PT iP
i - 1P = i - 1T iP
Manipulator kinematics II
Manipulator kinematics III
위의 식에서 변환식을 유도하면
i – 1T = i - 1T RT QT PT
와 같이 표현할 수 있고, 이를 다시 표현하면
i – 1T = Rx(i - 1) Dx (a i - 1) Rz (i ) Dz(d i)
또는
i – 1T = Screwx(a i – 1, i –1) Screwz( i , d i )
여기에서 ScrewQ(r, )는 축 Q를 따라서 거리 r만큼의 전위와 같은 축의 주위로 만큼의 회전을 의미.
Manipulator kinematics IV
앞의 식들을 정리해서 일반식으로 정리하면
i – 1T =
• 일단 링크 계가 정의되고, 그에 상응하는 링크인자가 구해지면 링크 인자값을 사용하여 링크 변환 행렬을 구하고 링크 변환행렬을 서로 곱한 변환은 n개의 관절변수 모두의 함수가 된다.
Actuator space, joint apace
and Cartesian space I
• 관절공간 (Joint space) : n 자유도 Manipulator에 있는 모든 링크는 n개의 관절변수 조합으로 명시되는데 이 변수의 조합을 n 1 관절벡터 라고 한다. 이 관절벡터가 형성하는 공간을 관절공간이라 한다.
• 직각 관절공간(Catetian space) : 직교하는 축을 따라 위치와 방위를 측정하기위한 공간 (작업지향적공간: Task oriented space, 또는 구조공간 : Operational space)
• 기구학 관절은 어떤 종류의 Actuator에 의해서 가동 하는 것으로 가정하는데, 실제의 산업용 로봇에서는 Actuator에 대한 위치의 개념을 고려해서 해석해야 한다. 이런 Actuator에 대한 위치의 해석을 Actuator벡터라 하고 때때로 이 Actuator 벡터의 함수로 관절벡터를 계산한다.
Examples : Kinematics of
industrial robots
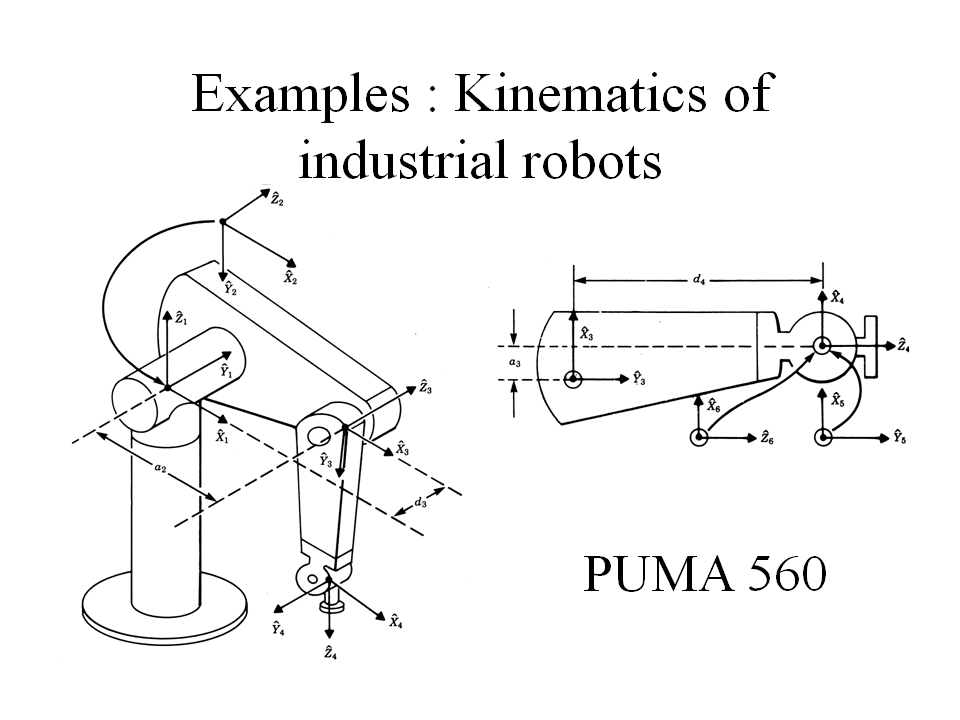
Examples : Kinematics of
industrial robots
각각의 링크인자가 구해지면 앞에서 설명한 링크 변환 행렬의 일반식에 적용하여 링크변환행렬을 구하고 이 행렬들을 곱해서 구해지는 변환행렬을 해석함으로써 기구학적인 해석 즉 계{0}을 기준으로 한 계{6}의 위치와 방향을 계산할 수 있다.
Px = c1 [ a2c2 + a3c23 – d4s23] – d3s1
Py = s1 [ a2c2 + a3c23 – d4s23] + d3c1
Pz = – a3s23 – a2s2 – d4c23
Examples : Kinematics of
industrial robots
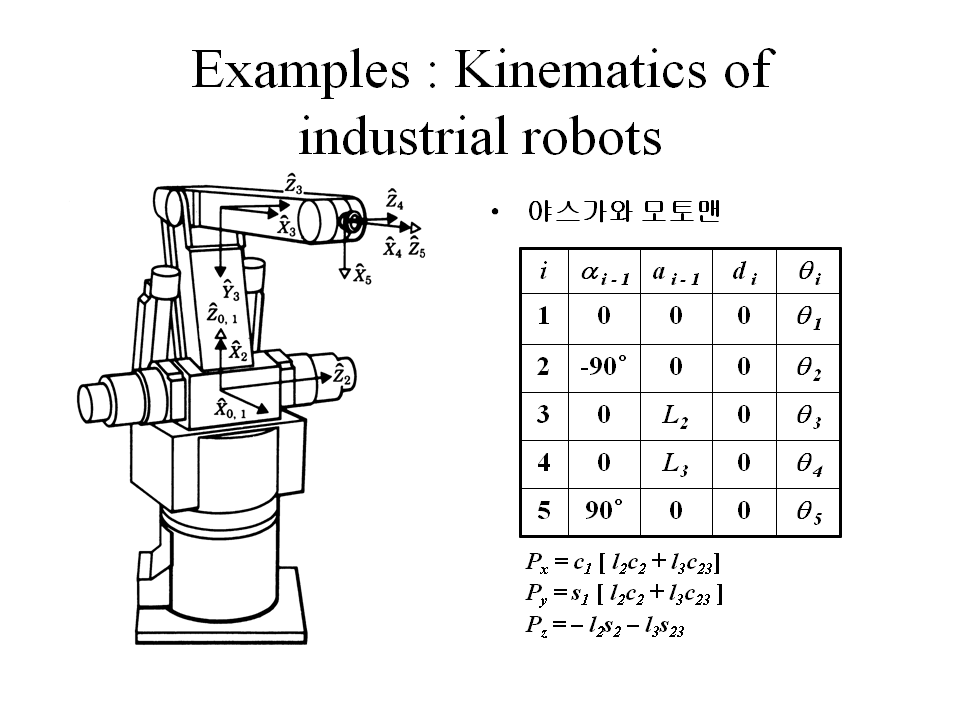
• 야스가와 모토맨
Px = c1 [ l2c2 + l3c23]
Py = s1 [ l2c2 + l3c23 ]
Pz = – l2s2 – l3s23
Frames with standard names I
• 기저계(The base frames : {B})
– Manipulator의 기저에 위치
- 단순히 계{0}의 다름 이름, 가끔 링크 0라고도 함
- 움직이지 않고 고정되어 있는 부분
• 정지계(The station frames : {S})
– 작업과제와 관련된 계, 로봇의 작업대 구석에 위치
– 로봇을 이용하는 사람의 입장에서는 {S}는 우주계이고 모든 로봇의 행동이 이 계를 기준으로 움직임
– 항상 기저계를 기준으로 명시됨
• 손목계(The wrist frames : {W})
– Manipulator의 마지막 링크에 위치
– 계 N의 다른 이름, {W}의 원점은 대부분 손목에 고정.
– 기저계를 기준으로 명시됨
Frames with standard names II
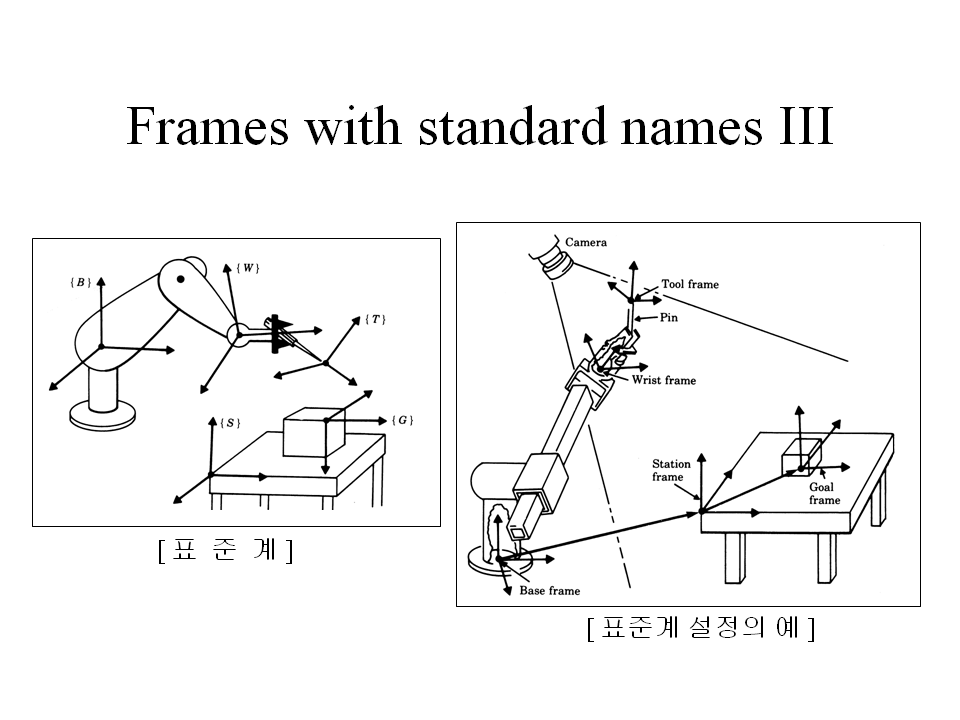
• 공구계(The tool frames : {T})
– 로봇이 들고 있는 공구의 끝에 고정
– 손이 비어 있을 경우 로봇의 손톱끝 중간에 원점설정
– 손목계를 기준으로 명시
• 목적계(The goal frames : {G})
– 로봇이 공구를 이동시키고자 하는 위치 표시
– 운동의 종료시 공구계와 목표계를 일치
– 정지계를 기준을 명시
Frames with standard names III
WHERE is the tool?
• 공구계 {T}값들을 정지계{S}를 기준으로 계산
• ST = BT-1 BT WT (WHERE함수)
• 팔이 어디에 있는가를 계산
• 출력결과는 작업대상으로부터 기준한 핀의 위치와 방위
• 링크의 기하학적 형태에 따른 기구학적 양을 계산
• 기저에서 일반화된 변환과 말단효과장치의 일반화된 변환을 계산
• 오프셋과 뒤틀림을 동반하는 공구를 고려할 수 있게 하고, 임의의 정지계를 기준 하여 동작할 수 있게 함
Computational consideration
• 관련된 수치값의 표현을 고정점 또는 가변점으로 하는 가에 대한 선택
– 가변점 : 변수의 상대적 크기를 스케일 할 필요 없음.
소프트웨어의 개발이 용이.
– 고정점 : 계산속도가 빠름.
변수들의 동적변화 범위가 넓지 않고 범위가 상당히 정확 히 알려짐.
• 방정식을 요소분해하면 경제적이다.
• 초월함수의 계산은 Look up table을 사용한다.
• 중복되는 계산은 피한다.
'myPPT' 카테고리의 다른 글
| 5 Efficient and Safe Weight Loss Methods (0) | 2022.07.08 |
|---|---|
| Digital Rights Management and Digital Watermarking (0) | 2022.06.29 |
| 화엄(華嚴)의 세계 (0) | 2022.05.08 |
| 콘크리트 역사 특징/ 성질 시험방법 / 시멘트의 종류와 그 특성 / 골재의 종류 및 성질 (0) | 2022.04.21 |
| 성격 (personlity) 과 능력(Ability) - MBTI(Myers-Briggs Type Indicator) / 빅파이브 모형 (0) | 2022.04.02 |
